公差原理
寛容原則、独立性の原則、最大実体、最小実体公差の要件
最大固体:実際の要素は、寸法公差の範囲内のほとんどの材料との状態を有します。
最小の固体:実際の要素は、寸法公差の範囲内であり、前記物質状態を有します。
最大固体サイズ:最大固体状態でのサイズ; 外表面(軸、ボスなど)の最大固形サイズが最大限界サイズに等しく、内部表面の最大固形サイズ(穴、スロット、など)が最小限界サイズに等しいです。
最小固体サイズ:最小固体でサイズ。外表面(軸、ボス等)の最小固形サイズが最小の限界サイズに等しく、内部表面の最小固形サイズ(穴、スロット、等)は、最大限界サイズに等しいです。
最大固体境界:最大固体状態で、理想的な形状との境界。
最小固体境界:最小固体状態で、理想的な形状との境界。
有効状態:図面及び要素の軸線又は中心平面の形状公差に所与測定素子の最大物理サイズにより形成された上限境界、および制限境界は、理想的な形状を有していなければなりません。
有効サイズ:実際の状態の境界サイズが最大固形サイズおよび形状公差の合成結果です。内面(孔、スロット、等)のための外部表面(シャフト、ボス等)、有効サイズ=上限サイズ 形状の公差のために、効果的なサイズが最小限界寸法形状公差を=。
寛容の原則とは何ですか?
寛容の原則は、寸法公差と幾何公差との関係を扱ったルールです。これは、三次元(線形および角度の)寛容と幾何公差との関係の原則を指定します。国家標準公差原理は、サイズ、形状、及び構成要素の位置特性を制約するために、次元の寸法、幾何公差のために技術的図面及び関連文書に適用されます。
寛容の原則は、独立の原則および関連の原則に分かれています。独立した原理がよりよく理解され、そして関連する原理はさらに公差要件、最大実体要件(およびその可逆性の要件)、最小実体要件(およびその可逆性の要件)に分割されます。
独立性の原則とは何ですか?
独立性の原理は、図面に与えられたそれぞれのサイズ及び形状要件(形状、向き、及び位置)が独立しており、要件は、それぞれ独自の限界を制御する、別々に満たさなければならないということです。寸法と幾何学的公差は独立の原則に準拠し、図面に特定の関係記号を追加しないこと。寛容、最大のエンティティ、および最小実体の原理は確かに少し複雑であるため、私たちの図面の大部分は、独立性の原則を使用して、仕事のこの局面では、多くのラベルがありません。ほとんどのサプライヤーは、あまりにもこれらの事を理解していません。もちろん、それはこれらの事は無用であることを意味するものではありません。ハイエンド、高精度の製品は、依然としてこれらの寛容の原則を考慮しなければなりません。
関連する原則は何ですか?
関連する原理は、図面上の所与の寸法及び幾何公差が互いに関連していることです。関連する要件は、公差要件、最大物理的要件(およびその可逆性の要件)、および最小物理的要件(およびその可逆性の要件)に分割されます。
インクルージョンの要件:
包含要件は、円筒面または二つの平行な対応として、単一の要素に適用されます。公差要件は、抽出された成分がそれらの最大の物理的な境界を越えてはならないことを示し、そのローカル実際の寸法は、最小の物理的寸法を超えてはなりません。公差要件を採用する単一の要素は、その寸法限界偏差又は公差域コードの後に記号「E」でマークされなければなりません。(一部の嵌合性質を確保する場合には、寸法公差および要素の形状の公差の関係は、実際の素子上の点が位置しなければならないれる寛容の原理に従って処理されなければなりません最大の固体境界サイズ)。実際の機能はどこでも最大固体境界に到達した場合は、任意の形状誤差があってはなりません。唯一最大の固体境界から実際の素子ずれた後、形状誤差は、所与の形状および位置公差によって制御することが可能となります。したがって、寸法公差、特徴の実際の大きさを制御するだけでなく、フィーチャの形状誤差を制限します)。
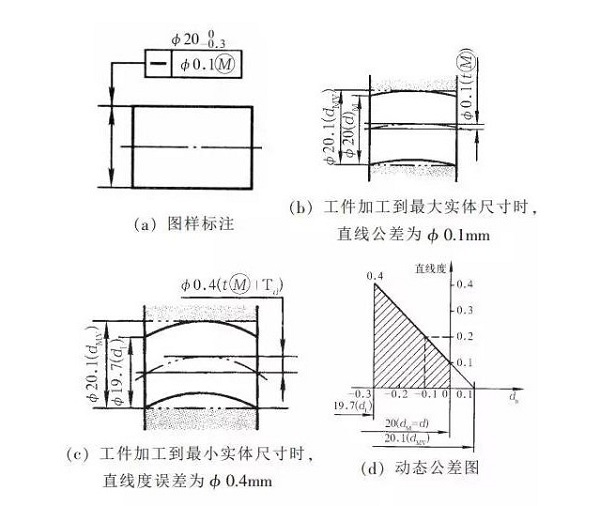
最大実体要件:
最大の物理的な要件は、形状及び位置公差が寸法公差に関連していることを示す公差要件です。測定または最大固体状態から基準要素ずれた場合、その形状及び位置公差は、寸法公差から補償することができます。記号は、図面上にマークされています。"M"。最大エンティティが測定素子および参照素子のために使用する必要がある場合、その寸法公差は、フォームおよび位置公差に補償されるが、それは最大のエンティティの実際の限界を超えることはできません。可逆要件が最大のエンティティに使用される場合、寸法公差と形状と位置公差は互いを補償することができます。
最小実体要件
最小実体要件は、フォームおよび位置公差が補償値を得ることができる許容要件である場合、最小実体状態から測定または基準要素ずれます。記号「L」は、図面に記されています。測定された要素は、基準要素と同時に最小物理的要件を採用することができます。このとき、形状及び位置公差は、二つの側面から補償することができます。