あなたはこれらの公差を理解してよろしいですか?
私たちは、図面に記さ公差を誤解した場合の生産では、それが結果と要件を処理し、処理し、分析を逸脱し、さらに深刻な影響をもたらすでしょう。
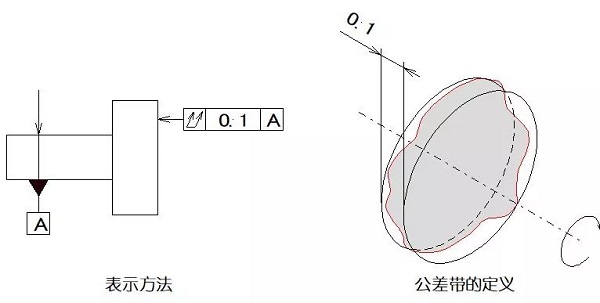
01真直度
一般に平坦と呼ばれる真直度は、理想的な直線部分が残っ上の線状要素の実際の形状ことを示しています。真直度公差が理想直線に対する実際のラインの最大許容変動です。
実施例1:指定された平面で、許容範囲は0.1mmの間隔を有する2本の平行な直線の間の領域内になければなりません。
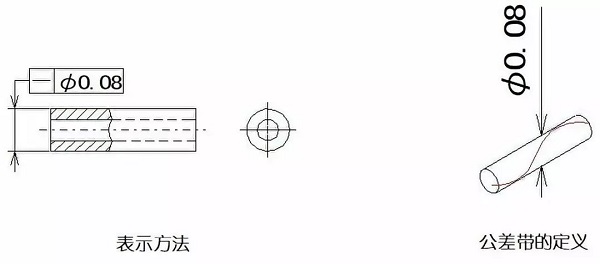
実施例2:許容値の前にマークΦを入れ、次いで、許容範囲は0.08ミリメートルの直径を有する円筒面の面積でなければなりません。
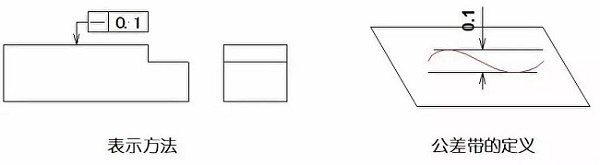
02フラットネス
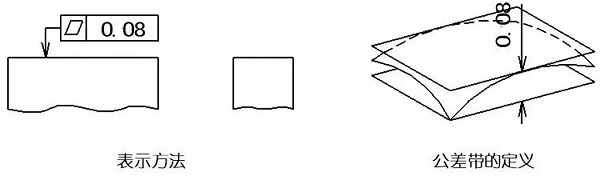
平坦度、いわゆる平坦性は、一部の平面状要素の実際の形状を示しており、理想的な平面を維持します。平坦度公差は、理想的な平面からの実際の表面の最大許容変動です。
例:許容範囲は、0.08ミリメートルの距離で2つの平行な平面の間の領域です。
03真円度
概して円形度と呼ばれる真円度は、一部の要素の実際の形状は、その中心から等距離に保たれることを示しています。真円度公差は、実際の円と同一の部分に理想円の間の最大許容変動です。
例:許容範囲が同じ正常部と0.03ミリメートルの半径の差を有する2つの同心円の間の領域上になければなりません。
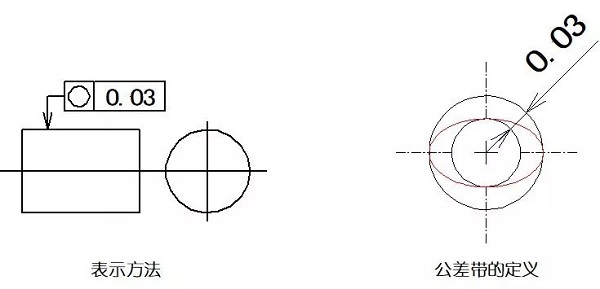
04円筒度
一部上の円筒面の輪郭上の点は、それらの軸から等距離に保たれる円筒手段。円筒公差は、理想的なシリンダに対向する実際のシリンダの最大許容変動です。
例:許容範囲は、0.1ミリメートルの半径の差を有する2つの同軸の円筒面の間の領域です。
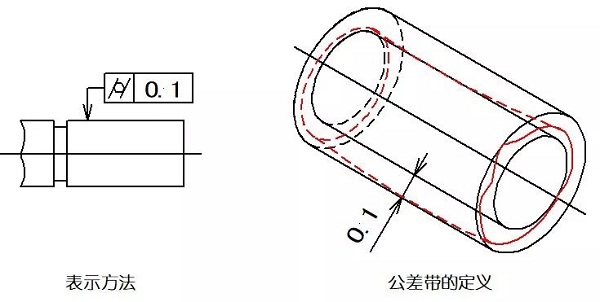
05ラインの輪郭
ラインの輪郭は、その理想的な形状を維持するために、一部の所定の平面上の任意の形状の曲線です。ライン輪郭公差は、非円形曲線の実際の輪郭の許容変動を指します。
例:公差域は、0.04ミリメートルの公差の直径を有する円のシリーズを包む2つの包絡線の間の領域です。円の中心は、理論的に正しいジオメトリを持つライン上に位置します。
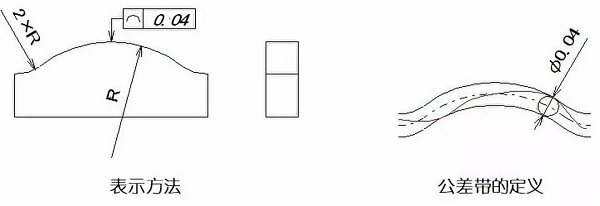
06顔の輪郭
顔の輪郭は、一部に任意の形状の曲面を示し、その理想的な形状を維持する状態です。表面輪郭公差は、非円形の湾曲した表面の実際の輪郭、及び理想輪郭表面の許容変動を指します。
例:許容範囲は、0.02ミリメートルの直径を有する球の一連の2本のエンベロープラインを包むことによって形成されます。球の中心は、理論的には、理論的に正しいジオメトリの表面上にあるべきです。
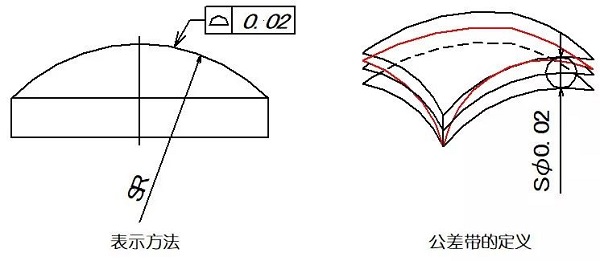
07並列
一般に、並列度として知られている並列処理は、一部に測定された実際の要素は、基準から等距離に保たれていることを示しています。平行度公差は、測定された要素の実際の方向と基準に理想的に平行な方向との間の最大許容変動です。
例:マークΦが許容値の前に追加された場合、許容範囲は基準平行直径Φ0.03mmの円筒面内にあります。
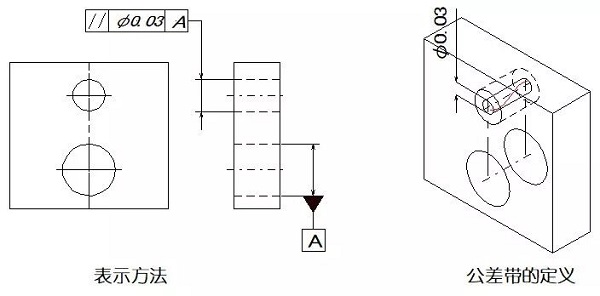
08垂直
一般に二つの要素が直交残る度合いと呼ばれる垂直は、一部に被測定素子は、基準素子に正しい90°の角度を維持することを示しています。直角度の公差は、測定要素の実際の方向と基準に対する理想的な方向垂直との間の最大許容変動です。
実施例1:公差域の前方にマークΦを入れ、次いで、許容範囲が基準面上の0.1ミリメートルの直径を有する円筒面に対して垂直です。
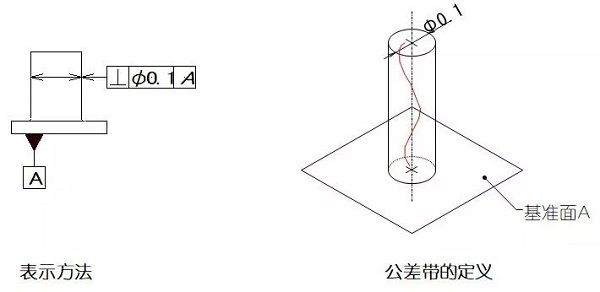
実施例2:許容範囲は基準線に対して0.08ミリメートルと垂直の距離を有する2つの平行な平面の間になければなりません。
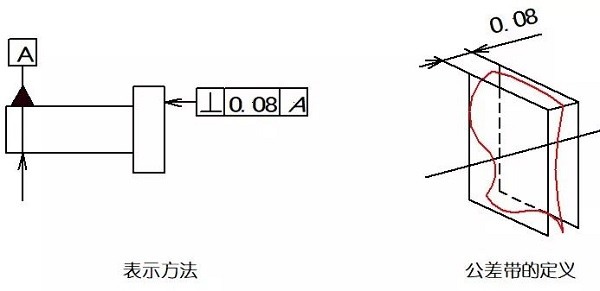
09チルト
傾斜部上の2つの要素は、互いに対して任意の角度に向いていることを示すために正しい状態です。傾斜公差を測定要素の実際の方向と任意の角度で基準の理想的な向きとの間の変化の最大許容量です。
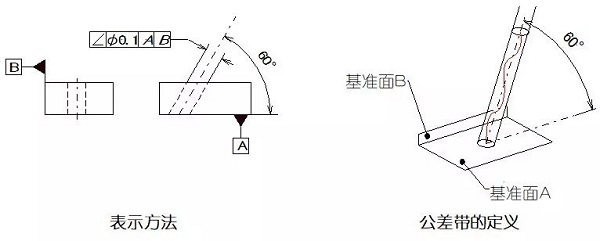
実施例1:測定軸の公差域は、基準面Aから0.08ミリメートルと60°の理論的な角度の間隔を有する2つの平行な平面の間の領域であります
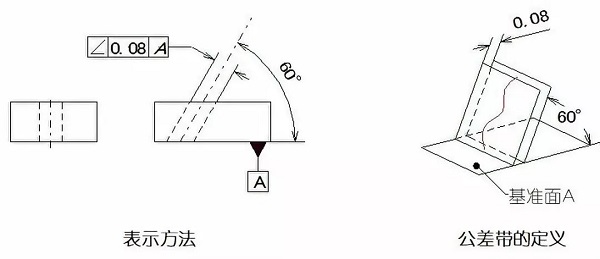
実施例2:許容値の前にマークΦを入れ、次いで、許容範囲が0.1ミリメートルの直径を有する円筒面内になければなりません。公差域は、データムA及びデータムAと60°の理論的に正しい角度で平面Bに垂直に平行でなければなりません
10ポジション度
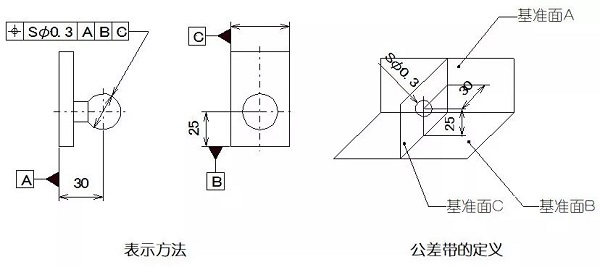
位置の程度は、その理想位置に対して部分に点、線、及び領域の精度です。位置公差は、理想的な位置に測定要素の相対的な実際の位置の最大許容変動です。
例:マークSφが許容ゾーンの前に添加する場合、許容範囲は、0.3ミリメートルの直径を有するボールの内側の領域です。ボールの公差域の中心点の位置は、基準A、B、およびCの理論的に正確な寸法を基準とし
11同軸(同心)度
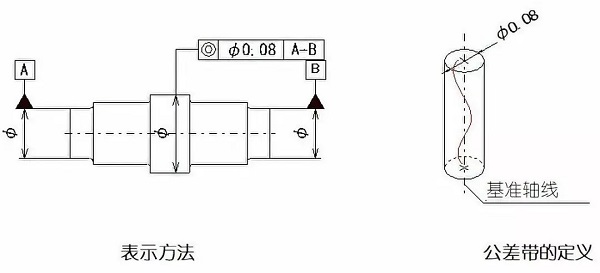
同心度は、一般に同軸の程度と呼ばれる、一部の測定軸が基準軸に対して同一直線に対して上に保持されていることを示しています。同軸公差は、基準軸に対して測定された実際の軸の許容変動です。
例:許容値がマークされている場合、許容範囲は、0.08ミリメートルの直径を有するシリンダとの間の領域です。円形の公差域の軸が原点に相当します。
12シンメトリー
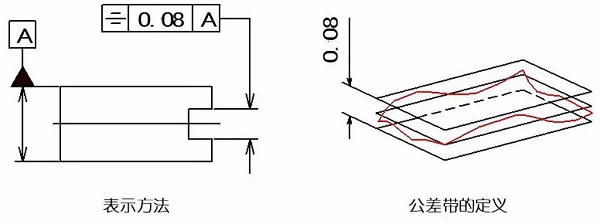
対称性は、一部に2つの対称中心要素は同一の中心面に保持された状態です。対称公差は、理想的な対称面に対して実際の素子の対称の中心面(又は中心線、軸)の許容変動です。
例:許容範囲は、基準中心面または中心線に対して対称に配置され2つの平行な平面または0.08ミリメートルの距離と直線との間の領域です。
13ラウンドの鼓動
円形の振れは、一部に回転面が基準軸に対して固定された位置に限定された測定面と遺跡内にある状態です。ラウンド振れ公差は、測定された実際の要素は、基準軸の周りに軸方向に移動せずに完全な円を回転させる限定された測定レンジ内の最大許容変動です。
実施例1:許容範囲は、0.1mmの半径の差と同じ基準の円の中心を有する2つの同心円の間の領域は、任意の測定面に垂直な軸です。
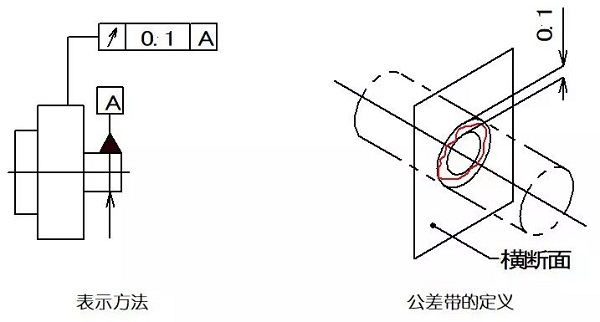
実施例2:許容範囲は、参照して任意の半径位置に同軸に測定する円筒面上に0.1mmの間隔を有する2つの円の間の領域です。
14のフル鼓動
一部が連続的に基準軸回りに回転されるとき、完全な振れ全体測定面に沿って振れの量を指します。完全振れ公差は、インジケータが、比較的理想の輪郭に沿って移動している間、それは連続的に基準軸回りに回転される測定された実際の要素の最大許容振れです。
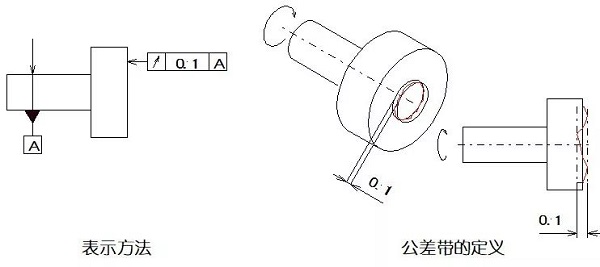
実施例1:許容範囲は0.1mmの半径差を有する基準と同軸である2つの円筒面の間の領域です。
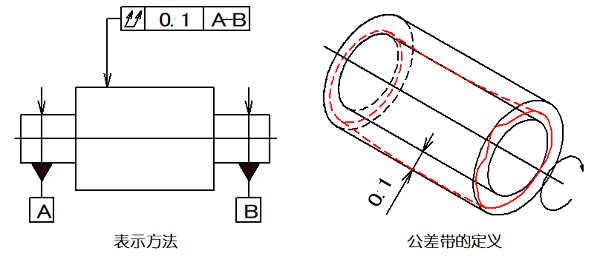
実施例2:公差域は、データムに対して半径と垂直に0.1mmの間隔を有する2つの平行な平面の間の領域です。